Олимпиадная задача по планиметрии: нахождение угла BCD в равнобедренном треугольнике
Задача
Угол при вершине A равнобедренного треугольника ABC (AB = AC) равен 20°. На стороне AB отложим отрезок AD, равный BC. Найдите угол BCD.
Решение
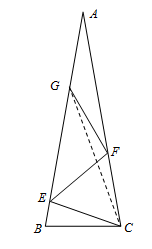
Решение 1:Поочерёдно построим на сторонах AB и AC точки E, F и G так, что BC = CE = EF = FG (см. рис. слева). Получатся равнобедренные треугольники BCE (с углом 20° при вершине E), CEF (с углом 60° при основании CF), EFG (с углом 100° при вершине F) и FGA (с углами 20° при основании FA).
AG = AD, поэтому точка G совпадает с точкой D. Так как треугольник CEF равносторонний, то треугольник CFG равнобедренный с углом 10° при основании, и ∠BCD = ∠BCG = 80° – 10° = 70°.
Решение 2:
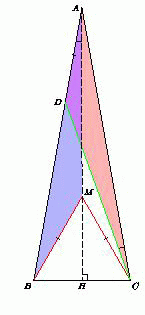
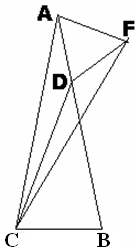
На высоте AH данного треугольника отметим такую точку M, что треугольник BMC – равносторонний (рис. в центре). Треугольники ABM и CAD равны по двум сторонам и углу между ними. Поэтому ∠ACD = ∠BAM = 10°. Следовательно, ∠BCD = ∠BCA – ∠ACD = 80° – 10° = 70°.Решение 3:Построим треугольник ACF, равный треугольнику BAC (рис. справа). Тогда треугольник ADF равносторонний, а CD – серединный перпендикуляр к отрезку AF, т.е. биссектриса угла ACF. Значит, ∠ACD = 10°. Далее как в решении 2.
Ответ
70°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь