Олимпиадная задача по планиметрии: Построение треугольника через точки на окружности
Задача
На окружности даны точки K и L. Постройте такой треугольник ABC, что KL является его средней линией, параллельной AB, и при этом точка C и точка пересечения медиан треугольника ABC лежат на данной окружности.
Решение
Пусть G – точка точка пересечения медиан треугольника ABC, N – точка пересечения медианы CP и средней линии KL (то есть N – середина KL). Тогда NG : NC = 1 : 3. Очевидно, достаточно построить точку С. Первый способ. По теореме о произведениях отрезков пересекающихся хорд ⅓ NC² = NG·NC = NK². Следовательно, C – точка пересечения данной окружности с окружностью радиуса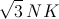 
с центром N.
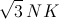
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет