Олимпиадная задача: Радиусы вписанных окружностей в треугольниках ABM и ACM (Планиметрия, 8–9 класс)

Предположим, что это так. Поскольку площади треугольников ABM и ACM равны, а радиус вписанной окружности треугольника ABM в два раза больше радиуса вписанной окружности треугольника ACM, то периметр треугольника ACM вдвое больше периметра треугольника ABM. Поэтому

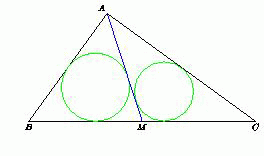
2(AB + BM + MA) = AC + CM + MA,  откуда  AC = CM + MA + 2AB > CM + MA,  что противоречит неравенству треугольника.

Не может.