Олимпиадная задача по планиметрии: трапеция и равные отрезки для 8-9 классов
Задача
При каком отношении оснований трапеции существует прямая, на которой шесть точек пересечения с диагоналями, боковыми сторонами и продолжениями оснований трапеции высекают пять равных отрезков?
Решение
Пусть указанная прямая пересекает продолжение меньшего основания AB трапеции ABCD, в точке E, боковую сторону AD – в точке F, диагональ BD – в точке G, диагональ AC – в точке H, боковую сторону BC – в точке I, продолжение основния CD – в точке J. Положим CJ = 2. Из подобия треугольников CJH и AEH находим, что AE = 3, а из подобия треугольников AEF и DJF получаем DJ = 12. Отсюда CD = 10. Из подобия треугольников CJI и BEI следует, что BE = 8. Значит, AD = 5.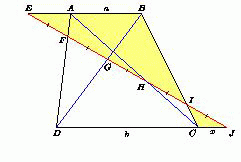 
Обратно, взяв трапецию с основаниями AB = 5, CD = 10 и отложив на их продолжениях отрезки AE = 3 и CJ = 2, аналогично проверим, что
EF = FG = GH = HI = IJ.
Ответ
1 : 2.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь