Олимпиадная задача по планиметрии для 8–9 классов: равновеликие треугольники в четырёхугольнике
Задача
Точки M и N – середины противоположных сторон BC и AD выпуклого четырёхугольника ABCD. Диагональ AC проходит через середину отрезка MN. Докажите, что треугольники ABC и ACD равновелики.
Решение
Пусть O – середина MN. Поскольку медиана разбивает треугольник на два равновеликих треугольника, то
SACD = 2SACN = 2(SAON + SCON) = 2(SAOM + SCOM) = 2SAMC = SABC. 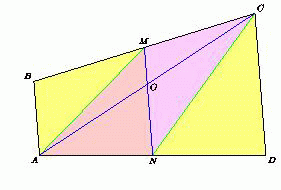
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет