Олимпиадная задача по планиметрии: параллельные стороны в остроугольном треугольнике

  Пусть AA₁, BB₁ и CC₁ – высоты треугольника ABC,  A₁C₁ || AC  и  A₁B₁ || AB.   Первый способ. Точки A₁ и C₁ лежат на окружности с диаметром AC. Поэтому AC₁A₁C – вписанная трапеция, значит, она равнобедренная, то есть  ∠A = ∠C.  Аналогично доказывается, что   ∠A = ∠B.

  Таким образом, треугольник ABC – равносторонний. Значит,  B₁C₁ || BC. 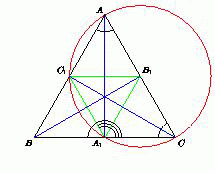   Второй способ. (A. Liu) Прямые CC₁ и BB₁ содержат высоты треугольника A₁B₁C₁. Значит, ортоцентры треугольников ABC и A₁B₁C₁ совпадают, откуда следует, что  AA₁ ⊥ B₁C₁,  то есть  B₁C₁ || BC.

Ответ задачи отсутствует