Олимпиадная задача по планиметрии для 8-9 классов: равносторонний треугольник внутри остроугольного

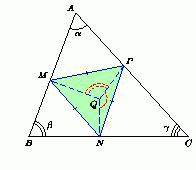
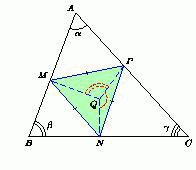
Решение 1:   Пусть внутри нашего треугольника ABC есть такая точка Q, о которой говорится в задаче. Обозначим проекции точки Q на стороны AB, BC и AC через M, N и P соответственно (см. рис.).

  Тогда  ∠MQP= 180° – ∠A,  ∠MQN= 180° – ∠B,  ∠NQP= 180° – ∠C.   По условию углыA, BиC– острые, поэтому углыMQP, MQNиNQP– тупые, причём их сумма равна 360°. ТреугольникMNQ– равносторонний (по предположению).   Рассмотрим теперь произвольный равносторонний треугольникXYZ. Пусть  ∠A≤ 60°  (такой угол в треугольнике всегда найдётся). В полуплоскости относительно прямойXY, содержащей точкуZ, построим дугу, из каждой точки которой отрезокXYвиден под углом, равным  180° – ∠A. Так как угол между касательной к этой дуге в точкеXи сторонойXYравен  ∠A ≤ 60°,  то вся эта дуга находится внутри треугольникаXYZ.   Далее построим дугу, из которой отрезок XZ виден под углом, равным  180° – ∠B.  Так как  ∠A + ∠B > 90° > 60°  (угол C – острый), то построенные дуги пересекаются в некоторой точке O, которая, как и вся первая дуга лежит внутри треугольника XYZ. Из точки O сторона YZ видна под углом

360° – (180° – ∠A) – (180° – ∠B) = 180° – ∠C.  Итак, существует, и притом только одна, такая точка O, из которой стороны треугольника XYZ видны под заданными углами.

  Теперь решим нашу задачу на построение. Через точки X, Y, Z проведём прямые, перпендикулярные отрезкам OX, OY и OZ. Точки пересечения этих прямых являются вершинами треугольника, подобного данному треугольнику ABC (у данного и построенного треугольника соответственно равные углы). Разделим стороны треугольника ABC в тех же отношениях, в которых точки X, Y и Z делят соответствующие стороны построенного треугольника. Точки деления и будут искомыми точками M, N и P.

Решение 2:   В обозначениях решения 1 точки M и P лежат на окружности с диаметром AQ. Поэтому  MP = AQ sin ∠ A.  Аналогично  MN = BQ sin ∠B,

NP = CQ sin ∠C.  Из равенства  MP = MN = NP  теперь следует, что  AQ·BC = BQ·AC = CQ·AB.  Геометрическим местом точек, удовлетворяющих первому равенству, является окружность Аполлония, проходящая через C и основания внешней и внутренней биссектрис угла C. Аналогично строится окружность – геометрическое место точек, удовлетворяющих второму равенству. Точка Q – общая точка этих окружностей, лежащая внутри треугольника ABC.

Ответ задачи отсутствует