Олимпиадная задача по планиметрии: точки касания и точка Нагеля в треугольнике
Задача
Докажите, что отрезки, соединяющие вершины треугольника с точками касания противоположных сторон с соответствующими вневписанными окружностями, пересекаются в одной точке {(точка Нагеля))
Решение
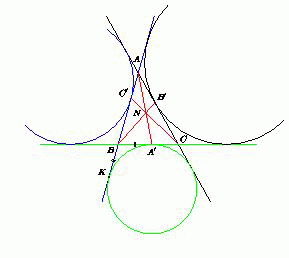
Рассмотрим треугольник ABC . Обозначим BC=a , AC=b , AB=a . Пусть A' , B' , C' – точки касания вневписанных окружностей треугольника со сторонами BC , AC , AB соответственно, K – точка касания первой из этих окружностей с продолжением стороны AB , p – полупериметр треугольника.
Тогда
BA'=BK = AK - AB = p-c.
A'C=p-b, CB'=p-a, B'A = p-c, AC'=p-b, C'B=p-a.
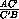 ·
· 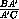 ·
· 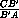 =
=
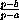 ·
· 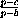 ·
· 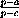 =1.
=1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет