Олимпиадная задача по планиметрии и стереометрии 8-11 класс: Клад на дне круглого озера
Задача
На берегу круглого озера растут 6 сосен. Известно, что если взять такие два треугольника, что вершины одного совпадают с тремя из сосен, а вершины другого – с тремя другими, то в середине отрезка, соединяющего точки пересечения высот этих треугольников, на дне озера находится клад. Неизвестно только, как нужно разбить данные шесть точек на две тройки. Сколько раз придётся опуститься на дно озера, чтобы наверняка отыскать клад?
Решение
Если A, B, C, D, E, F – произвольные точки, M и N – точки пересечения медиан треугольников ABC и DEF, то середина K отрезка MN – центр масс этих шести точек. Это означает, что при любом разбиении наших шести точек на тройки середина отрезка, соединяющего точки пересечения медиан таких треугольников, одна и та же.
Рассмотрим одно такое разбение: ABC и DEF (см.рисунок).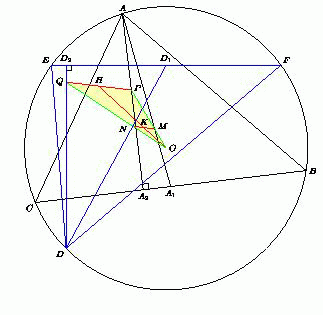
По условию все 6 точек лежат на окружности. Пусть O – её центр. Как известно, при гомотетии с центром в точке M и коэффициентом –2 центр O описанной окружности треугольника ABC переходит в ортоцентр P этого треугольника. При гомотетии с центром в точке N и коэффициентом –2 центр O описанной окружности треугольника DEF переходит в ортоцентр Q этого треугольника. Отсюда следует, что середина H отрезка PQ есть образ середины K отрезка MN при гомотетии с центром O и коэффициентом 3. Поэтому точка H не зависит от разбиения данных шести точек на две тройки. Таким образом, на дно озера достаточно опуститься один раз.
Ответ
Один раз.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь