Олимпиадная задача по теории чисел и индукции: камни в ящиках (Ященко, Гусейн-Заде)

  Заметим, что если выбрано число k, то после хода в ящике, в котором было m камней, будет  q + r  камней, где q и r – частное и остаток от деления m на k соответственно.

  Ясно, что достаточно рассмотреть ситуацию, когда в первом ящике лежит 1 камень, во втором – 2 камня и т. д. вплоть до n-го ящика, в котором лежит n камней (где  n = 460 или 461).   1) Пусть в ящиках лежат 1, 2, ..., n камней. Пусть выбрано число k и сделан ход а  f(n, k)  – максимальное число камней в ящике (после хода). Тогда для любого числа камней j,  1 ≤ j ≤ f(n, k)  найдётся ящик, в котором лежит j камней. Иначе говоря, числа камней в ящиках снова будут образовывать начальный отрезок натурального ряда.

  Докажем это обратной индукцией по j. Пусть найдётся ящик с j камнями. Тогда найдётся такое число  m  (1 ≤ m ≤ n),  что  j = q + r,   где q и r – частное и остаток от деления m на k. Если  r ≠ 0,  то в ящике, в котором был  m – 1  камень, станет  j – 1  камень. Если  r = 0,  то нужно рассмотреть ящик, в котором было  m – k камней.   2) Пусть частное от деления  n + 1  на k равно q. Рассмотрим ящик, в  (q – 1)k + (k – 1)  камней. В нём останется  q + k – 2  камня. Нетрудно видеть, что это будет самый большой ящик (впрочем, если  n + 2  делится на k, то будет еще ровно один ящик с таким же числом камней). Итак,

f(n, k) = q + k – 2 = [ⁿ⁺¹/_k] + k – 2.   Обозначим  m = ,  s = [m].   3) Оптимальное значение k (при котором  f(n, k)  достигает минимума) равно  s + 1.

  Доказательство.  f(n, k) = [ⁿ⁺¹/_k + k] – 2.  Функция  ⁿ⁺¹/_x + x  убывает на интервале    (0, m)  и возрастает на интервале   (m, n].  Так как [x] – неубывающая функция,  f(n, k)  достигает минимума либо при  k = s,  либо при  k = s + 1.

  Осталось доказать, что  f(n, s + 1) < f (n, s), то есть что  [ⁿ⁺¹/_s+1] < [ⁿ⁺¹/_s].

  Из неравенства  s² ≤ n + 1 < (s + 1)²  следует, что  [ⁿ⁺¹/_s+1] ≤ s,  а [ⁿ⁺¹/_s] ≥ s.  Значит, достаточно доказать, что обе части не могут равняться s. Но

[ⁿ⁺¹/_s] = s  ⇒  ⁿ⁺¹/_s < s + 1  ⇒   ⁿ⁺¹/_s+1 < s  ⇒  [ⁿ⁺¹/_s+1] < s.   4) Пусть  g(n) = f(n, s + 1).  Тогда, начиная с ящиков с 1, 2, ..., n камнями, мы при оптимальном выборе k (за один ход) получим ящики с 1, 2, ..., g(n) камнями.   Осталось убедиться прямым вычислением, что  g(g(g(g(g(460))))) = 1,  а g(g(g(g(g(461))))) = 2.

  Последовательность ходов для  n = 460  приведена в таблице:

  Если же в ящиках содержатся все наборы камней от 1 до 461, то после первого хода останутся, по крайней мере, все наборы от 1 до g(461) =f(461, 22) = 41;  после второго – все наборы от 1 доg(41) = 11; затем – от 1 до 5; от 1 до 3; и, наконец, от 1 до 2. Итак, при  n= 461  не всегда можно оставить по одному камню во всех ящиках.

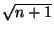
Ответ задачи отсутствует