Назад

Олимпиадная задача Канеля-Белова: Периметры квадратов и диагональ единичного квадрата

Задача 207996 • Сложность: 3 • 8-11 класс
Задача

Единичный квадрат разбит на конечное число квадратиков (размеры которых могут различаться). Может ли сумма периметров квадратиков, пересекающихся с главной диагональю, быть больше 1993? (Если квадратик пересекается с диагональю по одной точке, это тоже считается пересечением.)

Решение

  Разобьём единичный квадрат на четыре равных квадратика. Квадратики, пересекающиеся с диагональю только по вершине, назовём квадратиками первого уровня. Каждый из оставшихся квадратиков разобьём на четыре квадратика. Квадратики, пересекающиеся с диагональю по вершине, назовём квадратиками второго уровня. Снова разобьём каждый из оставшихся квадратиков на четыре квадратика и т.д. (см. рис.).

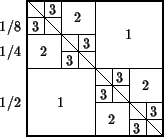
  Проведём эту операцию 500 раз. Мы получили 2k квадратиков k-го уровня. Сторона каждого из них равна 2–k. Значит, их суммарный периметр равен 4. Следовательно, суммарный периметр всех квадратиков всех уровней равен 4·500 > 1993.

Ответ

Может.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет