Задача по олимпиадной математике: Замок Мюнхгаузена и обход комнат (теория графов, индукция, 8-10 класс)
Задача
Дед барона К.Ф.И. фон Мюнхгаузена построил квадратный замок, разделил его на 9 квадратных залов и в центральном разместил арсенал. Отец барона разделил каждый из восьми оставшихся залов на 9 равных квадратных холлов и во всех центральных холлах устроил зимние сады. Сам барон разделил каждый из 64 свободных холлов на 9 равных квадратных комнат и в каждой из центральных комнат устроил бассейн, а остальные сделал жилыми. Барон хвастается, что ему удалось обойти все жилые комнаты, побывав в каждой по одному разу, и вернуться в исходную (в каждой стене между двумя соседними жилыми комнатами проделана дверь). Могут ли слова барона быть правдой?
Решение
Сначала обойдём один холл, например, по часовой стрелке (рис. слева). Рассмотрим соседний с ним холл и обойдём его аналогично. Для того чтобы обойти оба холла, достаточно поменять направление движения в двух парах клеток вдоль границы холлов (рис. в центре). Рассмотрим следующий холл, который граничит с уже обойдёнными. Поменяв направление движения аналогично предыдущему, получим способ обхода трёх холлов (рис. справа). Добавляя новые холлы по одному и меняя направление движения указанным образом, мы сумеем обойти весь замок.
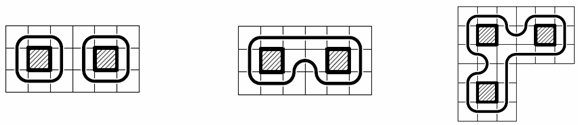
Ответ
Могут.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь