Олимпиадная задача по стереометрии и топологии: замкнутая цепочка шестерёнок
Задача
Можно ли в пространстве составить замкнутую цепочку из 61 одинаковых согласованно вращающихся шестерёнок так, чтобы углы между сцепленными шестерёнками были не меньше 150°? При этом:
для простоты шестёренки считаются кругами;
шестерёнки сцеплены, если соответствующие окружности в точке соприкосновения имеют общую касательную;
угол между сцепленными шестерёнками – это угол между радиусами их окружностей, проведёнными в точку касания;
первая шестерёнка должна быть сцеплена со второй, вторая – с третьей, и т. д., 61-я – с первой, а другие пары шестерёнок не должны иметь общих точек.
Решение
Требуемая конструкция изображена на рисунке.
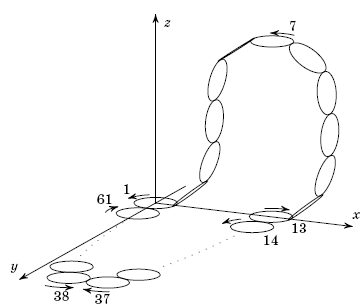
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет