Олимпиадная задача по планиметрии и комбинаторной геометрии для 7–9 класса: покрытие красного квадрата 100 белыми
Задача
Красный квадрат покрывают 100 белых квадратов. При этом все квадраты одинаковы и стороны каждого белого квадрата параллельны сторонам красного. Всегда ли можно удалить один из белых квадратов так, что оставшиеся белые квадраты все еще будут покрывать целиком красный квадрат? Комментарий. Во фразе "все квадраты одинаковы" имеется в виду, что все белые квадраты имеют тот же размер, что и красный.
Решение
См. рис. ниже для 8 белых квадратов.
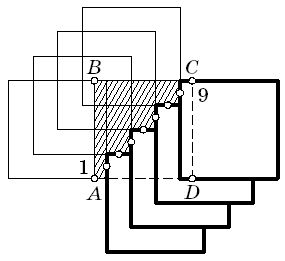
концы которых последовательно обозначим числами 1, 2, ..., 101 (точка A обозначена числом 1, а точка C — числом 101). Заметим, что для каждой пары точек k и k + 1 (k = 1, 2, ..., 100), существуют ровно два квадрата данного размера, стороны которых параллельны сторонам красного квадрата и проходят через точки k и k + 1, причем один из этих квадратов содержит вершину B и не содержит D, а другой квадрат, наоборот, содержит D и не содержит B (см. рис.). Если k нечетно, то возьмем тот квадрат, который содержит вершину B, а если k четно, возьмем квадрат, содержащий вершину D. Выбранные таким образом 100 белых квадратов покрывают целиком красный квадрат, но если удалить квадрат, стороны которого проходят через точки k и k + 1, то отрезок диагонали с концами k и k + 1 покрыт не будет.
Ответ
Не всегда.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь