Олимпиадная задача: первые цифры степеней пятерки и двойки для 10-11 класса

  Достаточно доказать, что любой начальный кусок последовательности первых цифр степеней пятерки встречается (в обратном порядке) в последовательности первых цифр степеней двойки.

  Рассмотрим числа: 2–1, 2^–2, ..., 2^–n. Последовательность первых ненулевых цифр их десятичных записей есть в точности последовательность первых цифр десятичных записей чисел 5, 25, ..., 5ⁿ. Таким образом, если добавить.

  Поэтому для решения задачи достаточно показать, что для любого k существует такая степень двойки  x = 2ⁿ,  десятичная запись которой имеет вид

1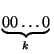y,  где y – оставшаяся часть десятичной записи. Иными словами,  x = 10^N + y,  причём  y < 10^N–k.   В этом случае  2^n–1= 2ⁿ: 2 = 500...0*,  2^n–2= 250...0*,  2^n–3= 1250...0*,  то есть  2^n–lсовпадает с первой цифрой числа 5^lпри  l < k.   Существование нужной степени двойки – частный случай задачи177898.

Ответ задачи отсутствует