Олимпиадная задача по планиметрии: наименьший периметр четырёхугольника

  Рассмотрим некоторый четырехугольникABCD. Перенесем его на вектор$\overrightarrow{AC}$(рис.). Получим четырехугольникA'B'C'D', гдеA'=C, а четырехугольникBB'D'D — параллелограмм, так как отрезкиBDиB'D'параллельны и равны. ПустьA₀,B₀,C₀иD₀— середины отрезковBD,BB',B'D'иD'Dсоответственно. Мы утверждаем, что A₀B₀C₀D₀ — параллелограмм, длины диагоналей которого равны длинам диагоналей четырехугольника ABCD, а угол между диагоналями равен углу между диагоналями четырехугольника ABCD. То,

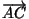
что A₀B₀C₀D₀ — параллелограмм, следует из того, что отрезки A₀B₀ и C₀D₀ — средние линии треугольников B'BD и B'D'D соответственно. Второе утверждение следует из того, что отрезки B₀D₀ и BD параллельны и равны также, как и отрезки A₀C₀ и AC.

Значит, осталось доказать, что периметр четырехугольника ABCD не меньше периметра параллелограмма A₀B₀C₀D₀. Но периметр параллелограмма равен B'D + BD' (по теореме о средней линии). По неравенству треугольника,

BC + CD'$\ge$BD' и  B'C + CD$\ge$B'D. Складывая эти неравенства, получаем нужное утверждение.

Ответ задачи отсутствует