Олимпиадная задача по планиметрии про ромб и угол DFC (7-9 класс, Волчкевич М. А.)

  Пусть прямые DE и AB пересекаются в точке G (см. рис.). Тогда треугольники DEC и BEG равны по второму признаку. Следовательно,  BG = CD = BA.  Далее можно рассуждать по-разному.   Первый способ. Точки A, G и C лежат на окружности с центром в точке B, причём AG – диаметр. Так как  ∠AFG = 90°,  точка F лежит на той же окружности.

  По теореме об угле, вписанном в окружность, имеем   ∠GFC= ½ ∠GBC= ½ (180° – 40°) = 70°.  Значит,  ∠DFC= 180° – ∠GFC= 110°.   Второй способ. Медиана FB прямоугольного треугольника AFG равна половине гипотенузы, то есть  BF = BA = BG.  Треугольники CBF и FBA равнобедренные, поэтому  ∠BCF + ∠BAF = ∠CFA.

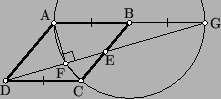
  Сумма углов четырёхугольника ABCF равна 360°. Поэтому  ∠CFA + ∠CFA + 40° = 360°,  откуда  ∠CFA = 160°.  Следовательно,

∠CFD = 360° – ∠AFC – ∠AFD = 360° – 160° – 90° = 110°.

Ответ задачи отсутствует