Олимпиадная задача по стереометрии: многогранник без трёх равных граней (10-11 класс)

  Будем искать многогранник с наименьшим числом граней. Из двух треугольников и двух квадратов нельзя

составить многогранник.

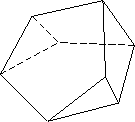
Шестигранник с двумя треугольными, двумя четырехугольными и двумя пятиугольными гранями сделать можно: расположим два пятиугольника с общим ребром в виде открытой ракушки, а щель заполним двумя треугольниками (по краям) и двумя четырехугольниками (рис.).

Такой многогранник получится, если у тетраэдра срезать две соседние вершины. Другое решение — срезать две соседние вершины у куба.

Комментарии. 1^o. На московской олимпиаде 1973 г. в 10 классе была родственная задача: "Докажите, что у любого выпуклого многогранника найдутся две грани с одинаковым числом сторон."

2^o. Подумайте над такой задачей: "Докажите, что в любом 10n- граннике найдутся n граней с одинаковым числом сторон".

Ответ задачи отсутствует