Олимпиадная задача по стереометрии и комбинаторике: Клетки на кубике Рубика 3x3x3
Задача
Поверхность кубика Рубика 3 x 3 x 3 состоит из 54 клеток. Какое наибольшее количество клеток можно отметить так, чтобы отмеченные клетки не имели общих вершин?
Решение
На рис. 1 показано, как отметить 7 клеток на трёх смежных гранях куба. На трёх "невидимых" гранях нужно отметить семь клеток, симметричных этим. Докажем теперь, что больше 14 клеток требуемым образом отметить невозможно. Сделаем это двумя способами. Первый способ.Посчитаем общее количество вершин клеток кубика Рубика. Имеются 8 вершин самого кубика, ещё по две вершины на каждом из 12 рёбер и ещё по 4 вершины на каждой из 6 граней. Итого: 8 + 122 + 64 = 56 вершин. Каждая из этих вершин принадлежит по условию не более, чем одной отмеченной клетке. Если бы отмеченных клеток было больше 14, то вершин было бы больше, чем 14*4 = 56, поскольку каждая клетка имеет 4 вершины. Значит, отмеченных клеток не более 14. Второй способ.Разрежем поверхность кубика Рубика на части. Три смежные грани разрежем на 7 частей, как показано на рис. 2. Три другие грани разрежем на такие же 7 частей. Легко видеть, что любые две клетки, попавшие в одну часть имеют общую вершину. Поэтому в каждой части может находиться не более одной отмеченной клетки. Значит, всего может быть отмечено не более 14 клеток.
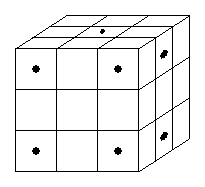 | 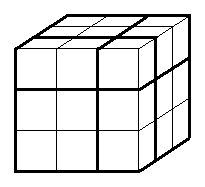 | |
| Рис. 1 | Рис. 2 |
Ответ
14 клеток.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь