Олимпиадная задача по последовательностям и алгебраическим методам для 7-9 классов
Задача
{a1,a2, ...,a20} — набор целых положительных чисел. Строим новый набор чисел {b0,b1,b2, ...} по следующему правилу: b0— количество чисел исходного набора, которые больше 0, b1— количество чисел исходного набора, которые больше 1, b2— количество чисел исходного набора, которые больше 2, и т.д., пока не пойдут нули. Докажите, что сумма всех чисел исходного набора равна сумме всех чисел нового набора.
Решение
Рассмотрим следующую конструкцию. Возьмем набор кубиков и будем строить из них "башенки" — столбики высотойa1,a2, ...,an(смотрите рисунок). Посчитаем двумя способами, сколько кубиков нам для этого понадобится. Считая по столбцам получаем, что количество кубиков равно сумме чисел первого набора. Другой способ подсчета — по слоям. Количество кубиков в первом слое (стоящих на полу) равноb0=n, в следующем слое —b1, и т. д., количество кубиков вi-м слое равноbi.
Поэтому общее число кубиков равно сумме чисел второго набора.
Значит, суммы чисел обоих наборов совпадают.
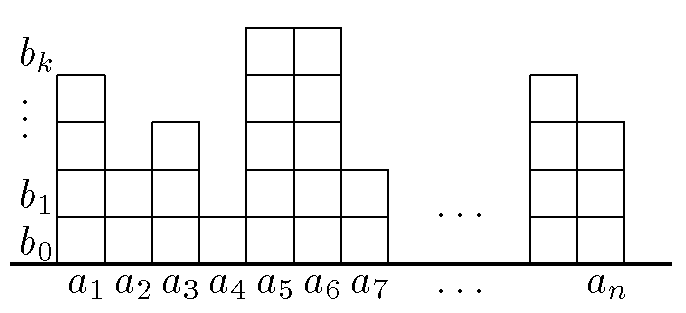
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь