Олимпиадная задача по планиметрии для 7-9 классов: равносторонний треугольник в задаче про треугольник ABC

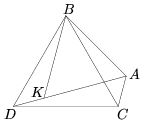
  Отметим на отрезке AD такую точку К, что  AK = AB  (см. рис.). Тогда по условию  KD = AC.  Треугольник ABK является равносторонним, поскольку он имеет две равные стороны и один из углов 60°. Поэтому треугольники ABC и KBD равны по двум сторонам и углу между ними  (∠BAC = ∠BKD = 120°).  Значит,  ВС = BD  и  ∠DBK = ∠CBA.  Добавив к обеим частям последнего равенства угол KBC, получаем  ∠DBC = ∠KBA.  Итак, треугольник DBC – равнобедренный с углом 60° при вершине, значит, равносторонний.

Ответ задачи отсутствует