Олимпиадная задача по планиметрии: хорды и диаметры круга для 7–9 классов
Задача
В круге провели несколько (конечное число) различных хорд так, что каждая из них проходит через середину какой – либо другой из проведённых хорд. Докажите, что все эти хорды являются диаметрами круга.
Решение
Заметим, что чем меньше расстояние от центраOокружности до хорды, тем больше длина хорды. Так как хорд конечное число, то среди них есть наименьшая по длине, скажем,AB. По условию, она проходит через серединуKнекоторой другой хорды, скажем,CD. Если точка пересеченияABиCDне является также и серединойAB, то расстояние от точкиOдоCDбудет, очевидно, больше, чем расстояние отOдоAB(т. к.OKбудет больше длины перпендикуляра, опущенного из точкиOнаAB), следовательно, хордаCDимеет меньшую, чемAB, длину — противоречие. Значит,CDпроходит через серединуAB, откуда перпендикуляры, опущенные из точкиOна эти хорды, совпадают. Это возможно, только еслиABиCDсовпадают, или еслиABиCDпересекаются в центре. Первое невозможно, значитABиCD— диаметры. Точно также доказывается, что все остальные хорды проходят черезO.
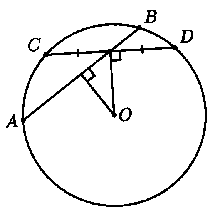 |
| Рис. 1 |
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь