Олимпиадная задача по планиметрии: деление стороны биссектрисой в трапеции ABCD

  Докажем, что биссектриса угла ABC делит сторону DC пополам.

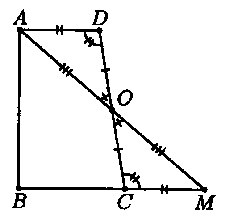
  Пусть O – середина стороны DC. Проведём через точки A и O прямую, пусть M – точка пересечения этой прямой с прямой BC. Тогда треугольники AOD и MOC будут равны по второму признаку, значит,  AO = OM,  AD = CM,  то есть треугольник ABM – равнобедренный. Но биссектриса при вершине равнобедренного треугольника является медианой и высотой, поэтому биссектриса угла B проходит через точку O.

Ответ задачи отсутствует