Геометрическое место середин оснований равнобедренных треугольников — олимпиадная задача планиметрии

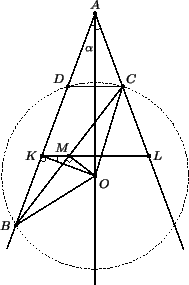
  Пусть A – вершина данного угла, O – фиксированная точка на биссектрисе, OBC – рассматриваемый равнобедренный треугольник  (OB = OC)  и M – середина стороны BC. Треугольник OBC может располагаться так, что  AB = AC.  При этом точка M лежит на биссектрисе AO, причём для любой точки M на биссектрисе AO, кроме точек A и O, можно построить равнобедренный треугольник OBC так, что M будет серединой отрезка BC. Таким образом, весь луч AO, кроме точек A и O, входит в искомое ГМТ.

  Пусть теперь  AB ≠ AC  (см. рис.). Пусть D – точка, симметричная точке C относительно биссектрисы AO. Тогда D лежит на луче AB и  OD = OC = OB.  Опустим перпендикуляр OK на BD. Так как  OB = OD,  то  BK = KD и, следовательно, KM – средняя линия треугольника BDC. Поэтому  KM || DC  и

KM ⊥ AO.  Таким образом, в этом случае точка M обязана лежать на таком отрезке KL, что L и C лежат по одной стороне угла,  OK ⊥ AB  и  KL ⊥ AO.

  Обратно, пустьM– любая точка указанного отрезкаKL, не лежащая на биссектрисе и отличная от точекKи L. Проведём черезMпрямую, перпендикулярнуюOM. Пусть она пересекает стороны угла в точкахBиC. Пусть  ∠BAO= ∠OAC= α.  Так как  OK⊥AB  и  KM⊥AO,  то ∠OKM= ∠BAO= α.  Так как  ∠BKO= ∠BMO= 90°,  то точкиB, K, M, Oлежат на одной окружности. Отсюда  ∠OBM= ∠OKM= α  (как вписанные). Тогда ∠OBC= α = ∠OAC  и, следовательно, точкиA, C, O, Bлежат на одной окружности. Так как   ∠BAO= ∠OAC= α,  то равны хордыBOиOC. Таким образом, треугольникOBC– равнобедренный и  BM = MC,  то естьMвходит в искомое ГМТ.

Биссектриса угла без его вершины и фиксированной точки, а также отрезок, соединяющий основания перпендикуляров, опущенных из фиксированной точки на стороны угла (без концов). На рисунке это луч AO без точек A и O и отрезок KL без точек K и L.