Назад

Олимпиадная задача по планиметрии: равнобедренные прямоугольные треугольники, 7–9 класс

Задача 205199 • Сложность: 2 • 7-9 класс
Задача

Треугольники ABC и A1B1C1 – равнобедренные прямоугольные (стороны AB и A1B1 – гипотенузы). Известно, что C1 лежит на BC, B1 лежит на AB, а A1 лежит на AC. Докажите, что  AA1 = 2CC1.

Разделы:
Планиметрия
Источники:
Московская математическая олимпиада 2006 год 8 класс Олимпиады и турниры
Количество версий:
5
Решение

  Первый способ. Обозначим  x = CC1,  y = CA1.   ∠CA1C1 + ∠CC1A1 = 90°  и  ∠BC1B1 + ∠CC1A1 = 90°  (рис. слева). Следовательно,  ∠ CA1C1 = ∠BC1B1.  Опустим перпендикуляр B1N на сторону BC. Треугольники B1NC1 и C1CA1 равны по гипотенузе и острому углу. Отсюда  B1N = x  и  NC1 = y.  Треугольник BNB1 – прямоугольный равнобедренный. Отсюда  NB = x.  По условию  y + AA1 = CA = CB = y + 2x.  Следовательно,  AA1 = 2x = 2CC1.

           
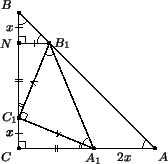
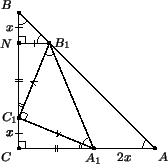
  Второй способ. Пусть D – середина стороны A1B1. Тогда  ∠C1DA1 = 90°.  Следовательно, четырёхугольник CC1DA1 – вписанный, откуда

∠DA1C1 = ∠DCC1 = 45°  и  ∠DC1C = ∠DA1A  (рис. справа). Таким образом, треугольники DC1C и B1A1A подобны по двум углам. Коэффициент подобия равен  B1A1 : DC1 = 2,  поэтому  AA1 = 2CC1.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет