Назад

Олимпиадная задача: минимальное нечётное количество ненулевых чисел в таблице 3×3

Задача 205198 • Сложность: 2 • 6-8 класс
Задача

В клетках таблицы 3×3 расставлены числа так, что сумма чисел в каждом столбце и в каждой строке равна нулю. Какое наименьшее количество чисел, отличных от нуля, может быть в этой таблице, если известно, что оно нечётно?

Разделы:
Текстовые задачи Доказательство от противного Алгебраические методы
Источники:
Московская математическая олимпиада 2006 год 8 класс Олимпиады и турниры
Количество версий:
4
Решение

  Пример.

 Оценка. Докажем, что меньшим количеством ненулевых чисел обойтись нельзя.   Если в таблице ровно одно ненулевое число, то сумма чисел в строке, содержащей это число, отлична от нуля.   Допустим, в таблице ровно три ненулевых числа. Если все они стоят в одной строке, то сумма чисел в любом столбце отлична от нуля. Если не все они стоят в одной строке, то в какой-нибудь строке стоит ровно одно ненулевое число, и сумма чисел в этой строке не равна нулю.   Допустим, в таблице ровно пять ненулевых чисел. Тогда в таблице стоит четыре нуля, значит, какие-то два нуля стоят в одной строке. Поскольку сумма чисел в этой строке равна нулю, все числа в этой строке – нули. Осталось заметить, что в столбце, в котором стоит оставшийся ноль, ровно два нуля, что невозможно.
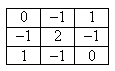
Ответ

7 чисел.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет