Олимпиадная задача по планиметрии и комбинаторной геометрии: разрезание фигур

а)Равносоставленностьлюбого треугольника и некоторого прямоугольника следует из рисунка ниже (прямаяlна рисунке содержит среднюю линию треугольника).

б) Докажем сначала, что любой параллелограмм равносоставлен прямоугольнику, одна сторона которого равна основанию параллелограмма, а другая — его высоте. Если высота параллелограмма падает на его основание, то его нужно разрезать по высоте (см. рис.).Если же она падает на продолжение основания, то тогда линиями, параллельными основанию, параллелограмм можно разрезать на параллелограммы, у которых высоты падают на основания. После этого каждый из полученных параллелограммов можно разрезать описанным выше способом (см. рисунок ниже). (Дотошный читатель сообразит, что последней оговорки можно было бы и не делать, поскольку всегда по крайней мере одна из высот параллелограмма падает на основание, а не на его продолжение; попробуйте доказать это самостоятельно.)Теперь перейдем к доказательству основного утверждения пункта б). Для любого прямоугольника можно найти параллелограмм, у которого:

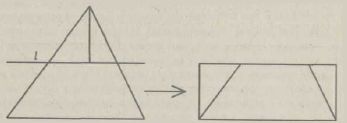
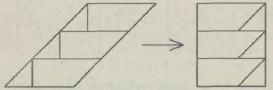
1. большая сторона равна большей стороне прямоугольника;
2. высота, опущенная на большую сторону, равна меньшей стороне прямоугольника;
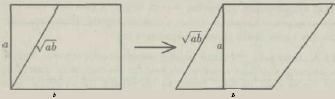
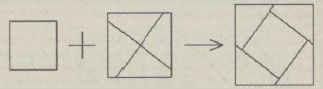
3. меньшая сторона равна опущенной на нее высоте. Способ построения такого параллелограмма приведен на рисунке ниже.
   
   Согласно доказанному утверждению, этот параллелограмм равносоставлен как исходному прямоугольнику, так и квадрату со стороной, равной его меньшей стороне. Значит, исходный прямоугольник равносоставлен квадрату. в) Докажем, что любой многоугольник можно разрезать на треугольники. Если многоугольник выпуклый, это очевидно — достаточно провести все диагонали из одной вершины. Если же он не выпуклый, то его можно разрезать на выпуклые, проведя продолжения всех его сторон. Согласно пунктам а) и б), каждый треугольник равносоставлен некоторому квадрату. Осталось доказать, что произвольные несколько квадратов можно разрезать на части, из которых можно сложить один квадрат. Как это сделать для двух квадратов, показано на рисунке нижу. Если квадратов больше двух, то проделав эту операцию с любыми двумя, мы уменьшим их количество на один. Повторяя ее, мы получим в конце концов один квадрат.
   

Верно.