Олимпиадная задача по стереометрии и планиметрии: тетраэдр с равными прямоугольными треугольниками
Задача
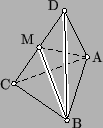
Существует ли тетраэдр, все грани которого — равные прямоугольные треугольники?
Решение
Предположим, что такой тетраэдр ABCD существует (см. рис.). Пусть AB – гипотенуза треугольника ABC. Тогда AB является также и гипотенузой треугольника ABD.
Ответ
Не существует.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет