Олимпиадная задача по планиметрии от Канеля-Белова: Бильярд на многоугольниках
Задача
Бильярдный стол имеет форму многоугольника (не обязательно выпуклого), у которого соседние стороны перпендикулярны друг другу. Вершины этого многоугольника – лузы, при попадании в которые шар там и остаётся. Из вершины A с (внутренним) углом 90° выпущен шар, который отражается от бортов (сторон многоугольника) по закону "угол падения равен углу отражения". Докажите, что он никогда не вернётся в вершину A.
Решение
Если шар вылетит из A по стороне, он свалится в ближайшую лузу. Пусть шар вылетел под острым углом к стороне AB. Легко убедиться, что при отражении как от параллельной, так и от перпендикулярной к прямой AB стороны наименьший угол между AB и звеном траектории не меняется (см. рис.). Через точку A проходит две прямые под таким углом к AB, но только вдоль одной из них шар, вылетев из A, внутрь стола. Поэтому вернуться в A шар может только пройдя по стартовому звену в обратном направлении.
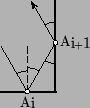
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь