Олимпиадная задача Толпыго А. К. о коэффициенте силы на шахматном турнире
Задача
Участники шахматного турнира сыграли друг с другом по одной партии. Для каждого участника A было подсчитано число набранных им очков (за победу дается 1 очко, за ничью – ½ очка, за поражение – 0 очков) и коэффициент силы по формуле: сумма очков тех участников, у кого A выиграл, минус сумма очков тех, кому он проиграл.
а) Могут ли коэффициенты силы всех участников быть больше 0?
б) Могут ли коэффициенты силы всех участников быть меньше 0?
Решение
Обозначим сумму очков, набранных i-м участником, через Si, а его коэффициент силы – через Fi. а) Первый способ. Достаточно доказать, что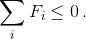 
Пусть S – среднее число набранных очков (такое число очков будет у игрока, завершившего все партии вничью). Пусть i-й игрок выиграл на di партий больше, чем проиграл (di может быть и отрицательным). Тогда
Si = S + ½ di. Si входит в сумму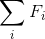 
с коэффициентом – di, поэтому
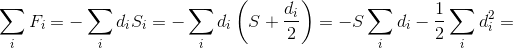
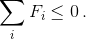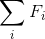( , очевидно, равна нулю). Второй способ. См. б). б) Fi можно представить как алгебраическую сумму, куда Sj входит с плюсом, если i-й игрок выиграл у j-го, и с минусом, если проиграл (Fi = 0, если все партии i-го игрока – ничьи).
Заметим, что сумма всех произведений SiFi равна нулю (действительно, произведение SiSj возникает в этой сумме дважды: как часть суммы SiFi и как часть SjFj, причём с противоположными знаками). Так как все числа Si неотрицательны и не все равны нулю, то либо все Fi – нули, либо среди них есть числа разных знаков.
Ответ
а), б) Не могут.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь