Олимпиадная задача про кузнечика на квадратном лугу: планиметрия и индукция
Задача
На лугу, имеющем форму квадрата, имеется круглая лунка. По лугу прыгает кузнечик. Перед каждым прыжком он выбирает вершину и прыгает по направлению к ней. Длина прыжка равна половине расстояния до этой вершины.
Сможет ли кузнечик попасть в лунку?
Решение
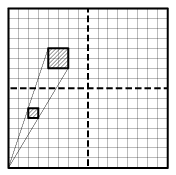
Достаточно доказать следующее утверждение. Пусть каждая сторона квадрата имеет длину 1 и разделена на 2n равных частей (n > 0), а через точки деления проведены прямые, параллельные сторонам. Тогда кузнечик сможет попасть в любую из 4n полученных клеток. При n=0 факт тривиален. Проведем индуктивный переход от n к n+1. Рассмотрим какую-то из клеток размера 4-n-1.Выберем самую близкую к ней вершину исходного квадрата и выполним гомотетию с центром в этой вершине и с коэффициентом 2. Тогда выбранная клетка перейдет в одну из клеток размера 4-n. По предположению индукции, кузнечик может в нее попасть. Если он прыгнет теперь на половину расстояния до указанной вершины, то он попадет в нужную клетку.
Источники и прецеденты использования
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь