Олимпиадная задача по стереометрии о правильном октаэдре и суммы расстояний до плоскостей граней
Задача
Грани правильного октаэдра раскрашены в белый и черный цвет. При этом любые две грани, имеющие общее ребро, покрашены в разные цвета.
Докажите, что для любой точки внутри октаэдра сумма расстояний до плоскостей белых граней равна сумме расстояний до плоскостей черных граней.
Решение
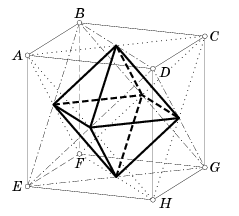
Плоскости, которым принадлежат грани каждого цвета, в пересечении образуют равные правильные тетраэдры. Чтобы доказать это, Рассмотрим куб ABCDEFGH (см. рис.) и два тетраэдра: ACFH и BDEG. Пересечение этих тетраэдров есть октаэдр. Действительно, вершины пересечения есть середины граней куба, а середины граней куба являются вершинами октаэдра.
Черные грани октаэдра лежат на одном тетраэдре, а белые – на другом.
Далее утверждение задачи следует из того, что сумма расстояний от внутренней точки правильного тетраэдра до его граней постоянна и равна утроенному объему тетраэдра, деленному на площадь грани.
Докажем последнее утверждение. Пусть A, B, C и D – вершины тетраэдра, O – точка внутри тетраэдра, hA, hB, hC и hD – расстояния от точки O до плоскостей BCD, ACD, ABD и ABC соответственно. Пусть S – площадь грани тетраэдра ABCD. Тогда объемы тетраэдров BCDO, ACDO, ABDO и ABCO равны (1/3)ShA, (1/3)ShB, (1/3)ShC и (1/3)ShD соответственно. Поэтому объем тетраэдра ABCD равен
(S/3)(hA+hB+hC+hD),
откуда следует требуемое утверждение.
Источники и прецеденты использования
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь