Олимпиадная задача по математике от Канель-Белова: средние величины, инварианты, 7-9 класс
Задача
На доске в лаборатории написаны два числа. Каждый день старший научный сотрудник Петя стирает с доски оба числа и пишет вместо них их среднее арифметическое и среднее гармоническое. Утром первого дня на доске были написаны числа 1 и 2. Найдите произведение чисел, записанных на доске вечером 1999-го дня.
Решение
Произведение чисел на доске не меняется. Действительно,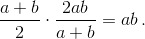 
Поэтому искомое произведение равно 2.
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет