Олимпиадная задача по планиметрии: биссектриса угла треугольника ABC, 7-9 класс

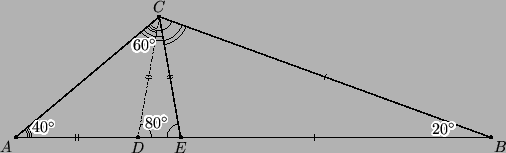
Отложим на стороне AB отрезок BD, равный BC. Тогда треугольник BCD – равнобедренный с углом при вершине 20°, поэтому углы при основании равны 80° (см. рис.). Пусть CE – биссектриса угла C. Тогда  ∠BCE = 60°,  поэтому  ∠AEC = 20° + 60° = 80°.  Таким образом, в треугольнике DEC равны два угла, поэтому он равнобедренный. Угол при его вершине C равен 20°, поэтому  ∠ACD = 40°.  Значит, треугольник ACD также равнобедренный, следовательно,

CE = CD = AD = AB – BC = 4.