Олимпиадная задача по планиметрии: стираем точки для минимизации квадратов

  в) Всего данные точки образуют 20 квадратов: 9 со стороной 1, 4 со стороной 2, 1 со стороной 3, 4 со стороной 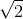    и 2 со стороной  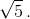   Обозначим точки буквами (рис. 1) и подсчитаем вершиной скольких квадратов является каждая точка (рис. 2).

 FGJK– квадрат, поэтому одна из его вершин стерта. Можно считать, что этоF. В результате "разрушено" 6 квадратов. На рис. 3 указано по сколько квадратов осталось "сидеть" на каждой точке.  GLOJ– квадрат, поэтому одна из его вершин стерта. Можно считать, что этоGилиL.   В первом случае "разрушено" ещё 4 квадрата. Осталось 10. Но на каждой из оставшихся точек "сидит" не больше трёх из оставшихся квадратов (рис. 4). Поэтому нужно стереть ещё по крайней мере 4 точки.   Во втором случае "разрушено" ещё 5 квадратов. Осталось 9. Если мы хотим стереть ещё только 3 точки, то на каждой из них должно "сидеть" по 3 квадрата, и все эти 9 квадратов должны быть различны. Но нетрудно проверить, что какие бы три из шести "трёхквадратных" точек мы не взяли (рис. 5), найдутся две из них, являющихся вершинами одного квадрата. Поэтому и в этом случае придется стереть ещё 4 точки.

а) Например, см. рис. слева.   б) Например, см. рис. справа.   в) 6 точек.