Олимпиадная задача Шарыгина: команды борцов и их победы, 7 класс, сложность 3
Задача
Есть девять борцов разной силы. В поединке любых двух из них всегда побеждает сильнейший. Можно ли разбить их на три команды по три борца так, чтобы во встречах команд по системе "каждый с каждым" первая команда по числу побед одержала верх над второй, вторая – над третьей, а третья – над первой?
Решение
Упорядочим наших борцов по силе и присвоим каждому рейтинг от 9 до 1. Тогда сумма рейтингов борцов равна 45. Постараемся составить команды так, чтобы суммы рейтингов борцов в командах были равны. Нарисуем магический квадрат 3×3 и рассмотрим его строки. Это три команды с одинаковым суммарным рейтингом – 15.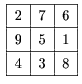 
Проверим. Первая со второй – счёт 5 : 4, вторая с третьей – счёт 5 : 4, и третья с первой – счёт 5 : 4!
Ответ
Можно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь