Наименьшая сторона треугольника — олимпиадная задача по планиметрии, 8-9 класс
Задача
Площадь треугольника равна 6$\sqrt{6}$, периметр его равен 18, расстояние от центра вписанной окружности до одной из вершин равно ${\frac{2\sqrt{42}}{3}}$. Найдите наименьшую сторону треугольника.
Решение
Пусть O — центр окружности, вписанной в данный треугольник ABC, r — её радиус, S = 6$\sqrt{6}$ — площадь, 2p = 18 — периметр, M — точка касания со стороной AC.
Поскольку S = p . r, то
r = $\displaystyle {\frac{S}{p}}$ = $\displaystyle {\frac{12\sqrt{6}}{9}}$ = $\displaystyle {\frac{2\sqrt{6}}{3}}$.
Из прямоугольного треугольника AOM находим, что
AM = $\displaystyle \sqrt{AO^{2}-OM^{2}}$ = $\displaystyle \sqrt{\left(\frac{2\sqrt{42}}{3}\right)^{2}-\left(\frac{2\sqrt{6}}{3}\right)^{2}}$ = $\displaystyle {\textstyle\frac{2}{3}}$ . $\displaystyle \sqrt{42-6}$ = 4.
Из равенства AM = p - BC находим, что
BC = 9 - 4 = 5.
Обозначим CM = x. Из равенства CM = p - AB находим, что
AB = p - CM = 9 - x.
По формуле Герона
S = $\displaystyle \sqrt{p(p-BC)(p-AC)(p-AB)}$, или 6$\displaystyle \sqrt{6}$ = $\displaystyle \sqrt{9\cdot 4\cdot (5-x)\cdot x}$.
Из этого уравнения находим, чтоx= 2 илиx= 3. В первом случаеAB= 7,AC= 6. Во втором —AB= 6,AC= 7. Следовательно, в каждом из этих случаев сторонаBC= 5 — наименьшая.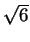
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет