Олимпиадная задача по планиметрии: площадь пятиугольника ABCDE, 8-10 класс
Задача
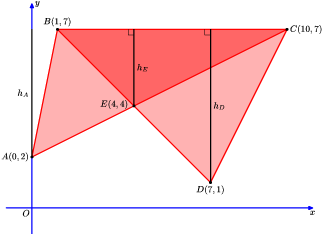
На координатной плоскости заданы точкиA(0;2),B(1;7),C(10;7) иD(7;1). Найдите площадь пятиугольникаABCDE, гдеE— точка пересечения прямыхACиBD.
Решение
Известно, что еслиy1$\ne$y2иx1$\ne$x2, то уравнение прямой, проходящей через точки(x1;y1) и(x2;y2), имеет вид
$\displaystyle {\frac{y-y_{1}}{y_{2}-y_{1}}}$ = $\displaystyle {\frac{x-x_{1}}{x_{2}-x_{1}}}$
Тогда уравнение прямой, проходящей через точкиA(0;2) иC(10;7) таково:
$\displaystyle {\frac{y-7}{2-7}}$ = $\displaystyle {\frac{x-10}{0-10}}$, или y = $\displaystyle {\textstyle\frac{1}{2}}$x + 2,
а уравнение прямой, проходящей через точкиB(1;7) иD(7;1) —
$\displaystyle {\frac{y-1}{7-1}}$ = $\displaystyle {\frac{x-7}{1-7}}$, или y = - x + 8.
Координаты точки пересечения прямыхACиBD— это решение системы
$\displaystyle \left\{\vphantom{ \begin{array}{lll}
y = \frac{1}{2}x+2\\
y = -x+8,\\
\end{array} }\right.$$\displaystyle \begin{array}{lll}
y = \frac{1}{2}x+2\\
y = -x+8,\\
\end{array}$
т.е.x= 4,y= 4. Таким образом,E=E(4;4).
Заметим, что
SABCDE = S$\scriptstyle \Delta$BAC + S$\scriptstyle \Delta$BDC - S$\scriptstyle \Delta$BEC.
ТреугольникиBAC,BDCиBECимеют общее основаниеBCи высотыhA= 7 - 2 = 5,hD= 7 - 1 = 6 иhE= 7 - 4 = 3. Следовательно,
SABCDE = $\displaystyle {\textstyle\frac{1}{2}}$ . (hA + hD - hE) . BC = $\displaystyle {\textstyle\frac{1}{2}}$ . (5 + 6 - 3) . 9 = 36.
Ответ
36.00
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет