Олимпиадная задача по комбинаторной геометрии: разрезание прямоугольника на квадрат
Задача
Дан картонный прямоугольник со сторонами a см и b см, где b/2 < a < b.
Докажите, что его можно разрезать на три куска, из которых складывается квадрат.
Решение
См. рис.
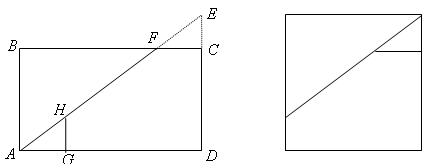
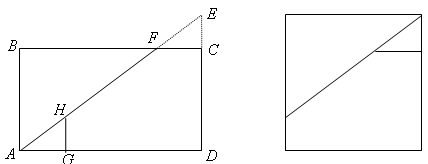), точки H и G – так, что треугольник AGH равен треугольнику FCE. При этом из полученных трёх частей автоматически складывается прямоугольник. Поскольку его площадь равна ab, а одна из сторон – , то это квадрат.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет