Олимпиадная задача по планиметрии для 8–9 класса: точка пересечения высот треугольника
Задача
Внутри треугольника ABC взята точка P так, что ∠ABP = ∠ACP, а ∠CBP = ∠CAP. Докажите, что P – точка пересечения высот треугольника ABC.
Решение
Решение 1:Пусть прямая AP пересекает сторону BC в точке D, а прямая CP пересекает сторону AB в точке E (рис. слева).
∠DPE = 180° – (∠ACP + ∠CAP) = 180° – ∠B, значит, четырёхугольник BDPE вписанный. Поэтому ∠ADE = ∠PDE = ∠PBE = ∠ACE, то есть четырёхугольник AEDC тоже вписанный. Следовательно, ∠CEA = ∠ADC = 180° – ∠ADB = ∠CEB, то есть CE – высота. Аналогично AD – высота.
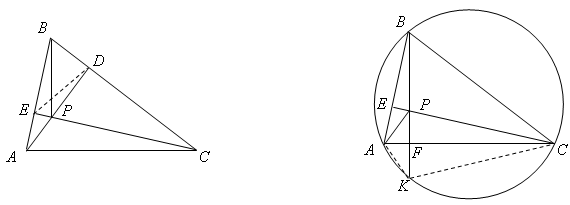
Решение 2:Пусть прямая BP пересекает сторону AC в точке F, а описанную окружность – в точке K (рис. справа). Треугольники APC и AKC равны по стороне и двум углам, поэтому треугольник PAK равнобедренный и его биссектриса AF является высотой. Значит, BF – высота треугольника ABC. Треугольники ABF и ACE имеют общий угол A и равные углы ABF и ACE, следовательно, ∠AFB = ∠AEC, то есть CE – тоже высота.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь