Олимпиадная задача по классической комбинаторике: доказательство для таблиц (10–11 класс)
Задача
Даны две таблицы A и B, в каждой m строк и n столбцов. В каждой клетке каждой таблицы записано одно из чисел 0 или 1, причём в строках таблиц числа не убывают (при движении по строке слева направо), и в столбцах таблиц числа не убывают (при движении по столбцу сверху вниз). Известно, что при любом k от 1 до m сумма чисел в верхних k строках таблицы A не меньше суммы чисел в верхних k строках таблицы B. Известно также, что всего в таблице A столько же единиц, сколько в таблице B. Докажите, что при любом l от 1 до n сумма чисел в левых l столбцах таблицы A не больше суммы чисел в левых l столбцах таблицы B.
Решение
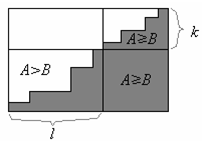
Предположим противное. Рассмотрим наименьшее l, при котором сумма l левых столбцов A превзошла аналогичную сумму B. Тогда в l-м столбце число нулей в A (обозначим его k) меньше, чем в B. Разрежем каждую из таблиц двумя перпендикулярными прямыми на 4 прямоугольные части (угла), отделив l столбцов слева и k строк сверху (см. рис. для таблицы A, где "зона единиц" показана темным). Сравним суммы в углах. В левых верхних углах обеих таблиц единиц, очевидно, нет. Поэтому сумма в левом нижнем углу равна сумме в l левых столбцах, и у A она больше по построению. Аналогично сумма в правом верхнем углу равна сумме в k верхних строках, и у A она не меньше по условию. Наконец, правый нижний угол A целиком заполнен единицами, поэтому сумма там не меньше. В итоге в А единиц оказывается больше, чем в B. Противоречие.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь