Олимпиадная задача по планиметрии и комбинаторной геометрии: 5 треугольников без поворота (8–9 класс, Шаповалов А. В.)
Задача
а) На столе лежат 5 одинаковых бумажных треугольников. Каждый разрешается сдвигать в любом направлении, не поворачивая. Верно ли, что всегда каждый из этих треугольников можно накрыть четырьмя другими?
б) На столе лежат 5 одинаковых равносторонних бумажных треугольников. Каждый разрешается сдвигать в любом направлении, не поворачивая. Докажите, что каждый из этих треугольников можно накрыть четырьмя другими.
Решение
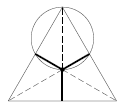
а) Рассмотрим, например, прямоугольный треугольник, у которого один катет в 5 раз больше другого. Четыре таких треугольника, расположенных так, что их больший катет горизонтален, очевидно, не смогут накрыть пятый, у которого больший катет вертикален. б) Докажем, что каждый треугольник можно накрыть даже тремя другими. Разобьём треугольник, который нужно накрыть, на три части, опустив перпендикуляры из центра треугольника на его стороны (см. рис.). Мы можем накрыть каждый из полученных четырёхугольников одним из данных треугольников, совместив центры вписанной окружности треугольника и описанной окружности четырёхугольника (как легко видеть, радиусы их равны).
Ответ
а) Неверно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь