Олимпиадная задача по планиметрии для 10–11 классов от Женодарова Р. Г.: треугольник ABC и расчёт отношения отрезков
Задача
Длины сторон треугольника ABC равны a, b и c (AB = c, BC = a, CA = b и a < b < c). На лучах BC и AC отмечены соответственно такие точки B1 и A1, что BB1 = AA1 = c. На лучах CA и BA отмечены соответственно такие точки C2 и B2, что CC2 = BB2 = a. Найти A1B1 : C2B2.
Решение
Пусть α = c : a. 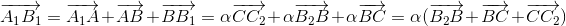
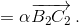
Ответ
c : a.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет