Олимпиадная задача по стереометрии и планиметрии: вершины n-угольника на кубе
Задача
Для какого наибольшего n можно выбрать на поверхности куба n точек так, чтобы не все они лежали в одной грани куба и при этом были вершинами правильного (плоского) n-угольника.
Решение
На одной грани куба не может лежать больше двух вершин многоугольника (в противном случае весь многоугольник лежал бы в этой грани). Поэтому многоугольник не может иметь больше 12 вершин.
Чтобы получить 12-угольник, вспомним, что существует сечение куба плоскостью, представляющее собой правильный шестиугольник. Это сечение проходит через середины шести рёбер куба (рис. слева). Действительно, "большие" диагонали сечения – отрезки, соединяющие середины противоположных рёбер куба, очевидно, проходят через центр куба и, следовательно, лежат в одной плоскости. Правильность шестиугольника следует из симметрии картинки.
Взяв на каждой из сторон правильного шестиугольника по две точки, деляших её в отношении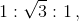 
мы, как легко проверить, получим вершины правильного 12-угольника (рис. справа).
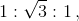
Ответ
n = 12.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь