Олимпиадная задача по делимости: максимальная последовательность чисел для условия сумм цифр
Задача
Найдите максимальное число N, для которого существуют такие N последовательных натуральных чисел, что сумма цифр первого числа делится на 1, сумма цифр второго числа – на 2, сумма цифр третьего числа – на 3, ..., сумма цифр N-го числа – на N.
Решение
Оценка. Будем обозначать сумму цифр числа a через S(a). Предположим что найдутся 22 последовательных числа a1, ..., a22, удовлетворяющие условиям задачи. Тогда числа S(a2), S(a12) и S(a22) чётны. С другой стороны, если предпоследняя цифра числа a2 не девятка, то S(a12) = S(a2 + 10) = S(a2) + 1. Противоречие. Если же предпоследняя цифра числа a2 – девятка, то предпоследняя цифра числа a12 – 0 и S(a22) = S(a12 + 10) = S(a12) + 1. Снова противоречие.
Пример из 21 числа. Пусть m = 5·7·8·11. Рассмотрим последовательные числа: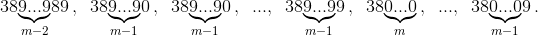 
Суммы цифр этих чисел равны 9m + 10, 9m + 2, 9m + 3, ..., 9m + 11, 12, ..., 21.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь