Олимпиадная задача по стереометрии для 10-11 классов от Шаповалова А. В.
Задача
В море плавает предмет, имеющий форму выпуклого многогранника.
Может ли случиться, что 90% его объёма находится ниже уровня воды и при этом больше половины его поверхности находится выше уровня воды?
Решение
Рассмотрим правильную пирамиду, плавающую вниз вершиной. Пусть площадь её боковой поверхности равна S. Тогда площадь основания равна S cos α, где α – угол наклона боковых граней к основанию. По условию под водой находится часть пирамиды, подобная исходной с коэффициентом подобия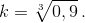 
Площадь боковой поверхности этой части равна k²S. Поскольку 2k² – 1 < 1, мы можем так выбрать угол α, чтобы выполнялось неравенство cos α > 2k² – 1. Но тогда 2k²S < S + S cos α, то есть под водой находится меньше половины поверхности пирамиды.
Ответ
Может.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь