Олимпиадная задача Канель-Белова: стратегия выигрыша в игре на квадрате 9×9
Задача
Игра происходит на квадрате клетчатой бумаги 9×9. Играют двое, ходят по очереди. Начинающий игру ставит в свободные клетки крестики, его партнер – нолики. Когда все клетки заполнены, подсчитывается количество К строк и столбцов, в которых крестиков больше, чем ноликов,и количество Н строк и столбцов, в которых ноликов больше, чем крестиков. Разность В = К – Н считается выигрышем игрока, который начинает. Найдите такое значение B, что
1) первый игрок может обеспечить себе выигрыш не меньше B, как бы ни играл второй игрок;
2) второй игрок всегда может добиться того, что первый получит выигрыш не больше B, как бы тот ни играл.
Решение
Решение 1: Одна из возможных стратегий первого игрока: первый ход в центр доски; далее каждый раз на ход второго в любую клетку он отвечает ходом в симметричную относительно центра клетку. Это возможно, поскольку симметрию каждый раз нарушает второй. В конечной позиции в каждой паре клеток, симметричных относительно центра, стоят крестик и нолик. Поэтому в центральной строке и в центральном столбце крестиков больше, чем ноликов; а каждой не проходящей через центр строке (столбцу) соответствует симметричная строка (столбец), причём в одной из них ноликов больше, а в другой меньше, чем крестиков. Таким образом, при этой стратегии выигрыш первого игрока равен 2. Теперь укажемстратегию второго игрока. Если у него есть возможность занять клетку, симметричную (относительно центра) клетке, только что занятой первым, он так и поступает. В противном случае он делает любой ход. При такой стратегии после хода второго множество занятых клеток либо симметрично (до тех пор, пока первый не занял центр), либо отличается от симметричного ровно в одной клетке. При этом в каждой паре занятых симметричных клеток будет находиться один крестик и один нолик. Своим последним ходом первый игрок вынужденно создаст позицию, описанную в предыдущем абзаце, и его выигрыш снова равен 2.
Решение 2: Разобьём доску на части так, как показано на рисунке. Стратегия первого: первым ходом занять левый нижний угол, а затем ходить в ту же часть доски, куда перед этим пошел второй.
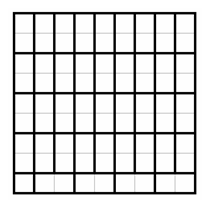
Ответ
B = 2.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь