Назад

Олимпиадная задача по планиметрии для 10-11 класса: четыреугольник и точки

Задача 198397 • Сложность: 3 • 10-11 класс
Задача

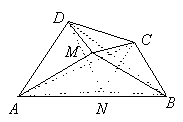
Внутренняя точка M выпуклого четырёхугольника ABCD такова, что треугольники AMB и CMD – равнобедренные с углом величиной 120° при вершине M.

Докажите существование такой точки N, что треугольники BNC и DNA – правильные.

Решение

  Будем для определенности считать, что обход вдоль границы четырёхугольника ABCD от A к B, C и затем к D совершается против часовой стрелки. Тогда при повороте на 120° в этом же направлении вокруг точки M точка A переходит в B, а точка C – в D. Значит, треугольник AMC переходит в треугольник BMD. Поэтому  AC = BD,  и угол между прямыми AC и BD составляет 120° (или, что то же самое, 60°).

  Рассмотрим правильный треугольникBNC, расположенный по ту же сторону от прямойBC, что и четырёхугольникABCD. При повороте на 60° против часовой стрелки вокруг точкиNточкаBпереходит вC. Значит, прямаяBDперейдёт в прямуюCA. Ввиду равенства отрезковCAиDBточкаDперейдёт вA. Таким образом,  NA = ND  и  ∠DNA= 60°,  то есть треугольникDNAтакже правильный.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет