Олимпиадная задача Рубанова: максимум диагоналей в разбиении квадрата на 25 клеток

  Пример с 16 диагоналями см. на рисунке.

 Оценка. Предположим, что удалось провести 17 диагоналей. Приведём два способа прийти к противоречию.   Первый способ. Каждая диагональ имеет два конца, расположенных в узлах квадратной сетки. Всего таких узлов в квадрате 36. 12 из них расположены на границе внутреннего квадрата 3×3 (рис. слева), поэтому диагоналей с концами в этих узлах проведено не больше 12. Оставшиеся пять диагоналей могут располагаться только в центральной и четырёх угловых клетках. Значит, четыре узла, расположенные в вершинах квадрата, не являются концами проведённых диагоналей, то есть 17 диагоналей имеют не более  36 – 4 = 32  концов. Противоречие.   Второй способ. В каждом прямоугольнике 5×2 проведено не больше 6 диагоналей: на его средней линии всего шесть узлов, а каждая диагональ имеет один из них своим концом. Значит, во всех горизонталях квадрата, кроме средней, проведено в сумме не более 12 диагоналей. Поэтому в средней горизонтали их не меньше, чем  17 – 12 = 5,  то есть в каждой её клетке проведена диагональ.

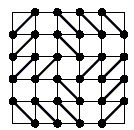
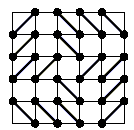
  Аналогично доказывается, что диагонали проведены во всех клетках средней вертикали. Но диагонали, проведённые в соседних (имеющих общую сторону) клетках, параллельны. Значит, весь "центральный крест" заполнен параллельными диагоналями. Но тогда диагонали в двух соседних с центром клетках имеют общую точку (см. рис. справа). Противоречие.

16 диагоналей.