Олимпиадная задача по планиметрии для 7-9 классов от Сендерова В. А.: биссектрисы и медианы в треугольнике
Задача
В треугольнике ABC отрезки CM и BN – медианы, P и Q – точки соответственно на AB и AC такие, что биссектриса угла C треугольника одновременно является биссектрисой угла MCP, а биссектриса угла B – биссектрисой угла NBQ. Можно ли утверждать, что треугольник ABC равнобедренный, если
а) BP = CQ;
б) AP = AQ;
в) PQ || BC?
Решение
Пусть BC = a, AC = b, AB = c. По условию СP – симедиана треугольника ABC. Значит, AP : BP = b² : a² (см. задачу 156978). Отсюда,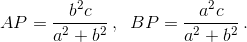 
Аналогично 
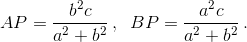а) Равенство BP = CQ можно записать в виде b³ + a²b = c³ + a²c ⇔ (b – c)(a² + b² + bc + c²) = 0. Поскольку второй множитель положителен, то b = c. б) Равенство AP = AQ можно записать в виде a²b + bс² = a²c + b²c ⇔ (b – c)(a² – bc) = 0. Оно выполняется не только в равнобедренном треугольнике (b = c), но и в треугольнике, стороны которого образуют геометрическую прогрессию (a² = bc), например, в треугольнике со сторонами a = 6, b = 4,
c = 9. в) AQ : QC = AP : PB ⇔ c² : a² = b² : a², то есть b = c.
Ответ
а) Можно, б) нельзя, в) можно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь